【中学数学】数列でつくってあそぼ(黄金比編)
好きな言葉は「近似」。どうもこんにちは、ジャムです。
今回は前回の最後に予告したとおり、「フィボナッチ・トリボナッチ数列」
を紹介していきたいと思います。
数列の記事なのにタイトルの黄金比とは何事だ、と思った人もいるかも知れません。
しかし、今回紹介するフィボナッチ数列は
黄金比と切っても切れない重要な関係を持っているのです。

トリボナッチ数列をおまけ程度に紹介していきます!
目次
フィボナッチ数列
フィボナッチ数列という変わった名前に驚いた人も多いことでしょう。
実は、この数列の発見者はレオナルド・フィボナッチという
イタリアの数学者なのです。
そんなフィボナッチ数列の説明をまずはしていきます!
フィボナッチ数列とは
今までに紹介してきた等差数列、階差数列というのは、
数列の種類を表す言葉でした。
しかし、フィボナッチ数列は数列の種類ではなく、
たった1つの数列に名前がついているものです。
まずはそのフィボナッチ数列をご覧ください。
一見不規則にも見えますが、実は面白い規則性があります。
少し考えてみてください。
わかりましたか?
実はこの数列、項の数字がその前の2つの項の合計となっているのです。

なんか意外な数列だと思います。
ちなみにこの数列は階差数列でも等差数列でもありません。
確かめれば分かるのですが、
項の差をとっても永遠に等差数列になることはありません。
では、数列の説明はこれぐらいにして、
黄金比との関係を見ていきましょう!
フィボナッチ数列と黄金比
黄金比は昔から美しい比率として知られてきた比です。
そんな比率とフィボナッチ数列との関係を知るには、
フィボナッチ数列の項の前後比に着目してみるのです。

よく見てみると、前後比は段々と1.6という数字に近づいていますね。
ここで、この数列を無限に続ければいつか1つの値に定まるのではないか、
と考えるのです。
その特定の値をとおいてみましょう。
このは無限にフィボナッチ数列を続けたときの項です。
(説明ヘタクソです....)
前後比ですから後の項の数字/前の項の数字ですよ!
さて、ここでフィボナッチ数列の約束を思い出してください。
フィボナッチ数列の項の数字は前の2つの項の数字の合計ですよね?
するとこの式はこんなふうに変形できます!
すると、の部分を約分して1とできますよね?
↑ちょっと工夫をして変形するとこんな式になります。
実はというのは前の項の数字/後の項の数字ですから、
前後比の逆数、すなわちの逆数なんです。
無限回続けたのに一項戻ったら無限じゃないんじゃない?
と思った人もいることでしょう。
実は、無限回数列を続けた場合、
たとえそこから1項(厳密には有限数項)戻しても
それもまた無限回数列を続けたことになります
(簡単に言えば、
そのため、今回の場合無限に数列を続けると
一定の値に定まる前後比の値も
1項戻した程度では変わりません!
(これを理解してくれる人が何人いるだろう...)
ということは、方程式がこんなふうになりますよね?
はい、出ました!2次方程式です。
ここまでくれば中学生でも解ける形式です。
では、解の公式を利用して解いてみましょう。
すると・・・
はい、これがフィボナッチ数列を無限に続けた時の前後比です!
これの値を求めると予想通り、
1.61801...という1.6に近い数字になります。
実はこの値こそ美しい比率、黄金比なのです。
(厳密には、のことを黄金比という。)
わかっていただけたでしょうか?
余談:黄金比に騙されるな!
あまり見る気がなければ次の項目へとお進みください。
さて、ここまで紹介してきた黄金比ですが、
しばしばこの比率は誤解を生んでいます。
例えばこちらの画像。

これはオウムガイの貝の写真なのですが、
しばしばこの貝殻の螺旋が黄金比となっている、と言う人がいます。
しかし、それは完全に嘘の情報です。
オウムガイの例もそうですが、
このように何でもかんでも黄金比に結びつける
インチキ数学のようなものも存在しています。
また、黄金比を使って(悪用して)人を騙して商売をしたりするような
悪い人たちもこの世にはたくさんいます。
ですからみなさん、くれぐれも黄金比のインチキには
騙されないでくださいね!
トリボナッチ数列
どうか仲良くしてやってください!
トリボナッチ数列とは
トリボナッチ数列は簡単に言えば
フィボナッチ数列を拡張したものです。
では、トリボナッチ数列はどのような数列なのかというと、
フィボナッチ数列を見てきた皆さんにはもうおわかりですね?
そうです、トリボナッチ数列とは、
項の数字がその前の3つの項の数字の合計となっている数列です!
しかし、この数列はフィボナッチ数列を
無理やり拡張したものに過ぎないので、
黄金比みたいなすごい比率との関わりはありません。
(まあトリボナッチ定数はあるけどさ.....)
トリボナッチ数列の"変な名前"の理由
これもあまり数列とは関係ないお話になってしまいます....
トリボナッチ数列と言う名前の由来ですが、
決してトリボナッチという人がいるわけではありません。
実はトリボナッチの"tri"とは3を表す接頭辞なんです。
それをフィボナッチ(人名)にくっつけたのがトリボナッチというわけです。
みなさん、人名に3をくっつけるというのはいかがなものか...
と思いません?
まとめ
黄金比に夢中になりすぎて、
記事がまあまあな量になってしまいました....
それに対するトリボナッチ数列の量が少なすぎて自分でもびっくりです。
これで4つの数列はすべて紹介し終わりました!
だから次回からはまた新しいネタ考えなきゃだめじゃねーか!
お疲れ様でした!
それでは!
【中学数学】数列でつくってあそぼ(階差数列編)
好きな言葉は「発散」。どうもこんにちは、ジャムです。
今回は前回に引き続き、主要な数列に触れていきます。
前回は等差数列を紹介しましたが、今回は階差数列と呼ばれる
数列について触れていきます。
本題に入る前に、前回の等差数列の例題をしてみましょう。
目次
等差数列の復習
例題
初っ端から開成の問題ですが、考えれば案外解けるので解いてみてください!
解答
どうですか?難しかったですかね?
この問題は等差数列を存分に用いて解く問題なので選んでみました。
(実は問題に出てくる数列そのものは階差数列)
解説は...すみません!
その気になったら書きます!(←おい)
階差数列
例題には正解できたでしょうか?
正解できた方も、残念ながら間違えてしまった人も、
階差数列について学んでいきましょう!
階差数列とは
とりあえず、wikiに書いてある定義を見てみましょう。
階差数列とは、ある数列に対し、隣り合う項の差をとることによってできる新たな数列のことである。
・・・
はい、はい、皆さんの言いたいことはわかります。
さっぱりわからん!
ということで、こちらも具体例で考えていきましょう!
次のような数列があるとします。
ここで、前回登場した等差数列ではないか、と疑えたあなた、
素晴らしいですね!
でもよく考えてみてください、項と項の差が一定ではありませんね。
では不規則なのかというと、そうではないんですね。
そこで、項と項の差に着目してみてください。
何かに気づきませんか?
そうです、等差数列です。

言葉では説明しにくいですが、
階差数列とは項と項との差が等差数列または新たな階差数列
となっている数列なのです!
項と項との差が新たな階差数列となっている例を1つ紹介します。
こちらの数列は、一度項と項との差を出してみても
等差数列にはなりません。

ただここで手を止めるわけではありません。
もう一度差を出してみるのです。
すると・・・

という具合に、階差数列は差を出していけば、いつかは等差数列になります!
そして上図のように差をとって表にしたものを階差表なんて言ったりします。
階差数列の和
階差数列の和の話ですが、階差数列には先程のように1度差をとれば
等差数列になるものもあれば、
何十回と差をとらなければ等差数列にならないものもあります。
そのため、階差数列の和の公式は存在していません。
そして、階差数列の和が入試で出るかといえば、
恐らくほとんど出ることがないものです。
ですから、折角このような項目を作りましたが、
階差数列の和については紹介しないことにします。
まとめ
今回は階差数列について紹介しましたが、
十分に理解できたでしょうか?
階差数列は高校入試より大学入試に出やすいでしょうから、
階差数列を深く掘り下げる必要はあまりありません。
しかし、等差数列の発展として紹介してみました。
次回は最後の2つの数列、「フィボナッチ数列,トリボナッチ数列」
について紹介するので乞うご期待!
それでは!
【中学数学】数列でつくってあそぼ(等差数列編)
好きな言葉は「収束」。どうもこんにちは、ジャムです。
今回紹介するのは、気づくことができれば得点源になる数列です。

数列と一言に言っても様々な数列があります。
全部で4つ紹介する予定なのですが、今回は
等差数列についてやっていきましょう!
目次
まず数列とは
数列というのは名前の通り数が列を成しているのですが、
いくつかの用語を知っておく必要があるので説明します。
用語
項
数列の最初の項を初項、最後の項を末項と呼びます。
また、それ以外のの項についても初項を第1項として順に、
第2項、第3項...という具合に呼びます。
そして、数列の項の数のことを項数といいます。
高校以上であれば、第項の数字を
と表記します。
数列の和
特定の項から別の特定の項までを足し合わせたものを、
数列の和(部分和)と呼びます。
数列の意味
数列の和(部分和)と呼びます。
数学では基本的に規則性のある数の列を数列と呼びます。
数列でない例
一切規則性のない数の列(数列ではない)
数列である例
正の奇数を並べたもの(数列である)
等差数列
数列の意味とそれに関する用語を理解したところで、
今回は等差数列に触れていきましょう!
等差数列とは
こちらの数列は言葉で説明するより、例で見るほうが
わかりやすいかもしれません。
念のために定義を説明すると、
という定義になっているのですが、例を見ないと
ちょっと理解しづらいですよね。
ということで、例を挙げてみます!
これは、先程数列の例として挙げた奇数を並べたものです。
さて、ここで問題です。
この数列の初項は何でしょう?
正解は1です。
初項とは最初の項のことなので、この場合一番最初の1を指します。
ちなみにこの場合の末項はありません。(無限に続いているから)
そしてこの数列は項が1つ進むごとに
数字が2ずつ大きくなっていますよね?
この等差数列の一定の差のことを公差と呼びます
(覚えなくてもいいです)。
等差数列の和
等差数列の和の求め方を紹介する前に世紀の天才ガウスの逸話を
紹介しましょう。
ある時、1 から 100 までの数字すべてを足すように
課題を出された。それを彼は、
1 + 100 = 101, 2 + 99 = 101, …, 50 + 51 = 101
となるので答えは 101 × 50 = 5050 だ、と即座に解答して教師を驚かせた。(wikiより)
実は、この話に登場する数列の正体、
初項1,公差1,項数100の等差数列なんです。
そんな数列を天才ガウスはあっという間に足し合わせてしまいました。
そんなガウスの使ったテクニックを数式化すると、

は初項,
は公差,
は項数,
は末項,
は第
項までの和
といっても何を言ってるかわからないと思うので、
先程のガウスの例で考えていきましょう。
まずガウスは初項の数と末項の数の和,
初項から1番目の数と末項から1番目の数の和,....
が101で一定であることに気づきました。
つまりこのまま数列の半分辺りまで足し算を続けて行けば、
単純な掛け算で数列の和を出せるのではないか、
と、ガウスは考えたわけです。

するとちょうど50+51のところで全部で
50組の101ができることになります。
そのためガウスは101に50をかけ合わせ、
だ、と言ったわけですね!
(説明がわかりにくくてすみません...)
しかもこれはこの場合によらず、例えば
のような場合でも
101+1=102, 99+3=102,...という具合に102が全部で50組できて、
51が1つ余ります。
ここで疑問が湧きますよね。余ってしまったものはどうするのか、と。
実はこの51という数字は組にした102という数字のになっていて、
余った場合絶対にそうなります。
なので、ここでは50.5組としてカウントするのです。
これを踏まえると組になる数字(先程の101や102)は
初項と末項の合計()、
組の数は項数のになることがわかります(
)。
それらをかけ合わせればすべての項を足し合わせた結果となるので
そして、末項は初項と項数から1を引いた値(項と項の"間"の数)に公差を
かけ合わせた数()との和なので、
末項の部分に式を代入して、

という公式が成り立つのです。
まとめ
等差数列の和の説明が無理やりになってしまいすみません...
実は4つの数列を全部一気に紹介する予定だったのですが、
文章量が半端なくなってしまったので分割させていただきました。(^^;
例題も次回まとめて載せますので、お楽しみに!(楽しみにしてる人はいないか...)
あとタイトルは気にしないでください
それでは!
【中学数学】覚えておくと得する三角比
好きな言葉は「稠密」。どうもこんにちは、ジャムです。
今回は、受験で役に立つ有名角の三角比について紹介していきたいと思います!

30°や45°などの辺の比については知っている人も多いかもしれませんが、
更に応用的なそれらの半角についても触れていきます!
高校以上であれば三角関数を使うところですが、
すでに高校数学を履修済みの人も、一度初心に帰ってみてください!
目次
有名角の三角比
まずは有名角の三角比についてです。
覚えておくと計算スピードが格段に上がるので、
有名角の三角比は最低限覚えておきましょう。
45°の三角比

45°の三角形は直角二等辺三角形として知られています。
一般的な二組の三角定規の片方の三角形でもあります。
そんな、45°の三角比は、

45°の直角三角形が二等辺三角形であることを踏まえれば、
三平方の定理を使って容易に求めることができます。
30°の三角比

こちらも45°同様に、三角定規の片方の三角形です。
こちらは正三角形を頂点から垂線をおろして、二分割した三角形です。
それを踏まえて三角比を算出すると、

これも先程の45°の直角三角形同様に、三平方の定理を用いれば、
容易に求めることができます。
説明は省略します。
有名角以外の三角比
さて、ここまで有名角の紹介でしたが、
ここからは少し発展的な半角の三角比を紹介したいと思います。
有名角の組み合わせで求めることができるので、
これらもしっかりと覚えておきましょう。
22.5°の三角比

こちらは45°の半角である22.5°の三角形。
これの三角比を求めるには少し補助線を付け足します。

どうでしょうか?なにか見えてきませんか?
実は、67.5°の部分を45°と22.5°にちょうどよく分割できるんですね~。
すると45°の三角比を使って比が出せそうですよね!

はい、出ました!
45°の三角比を利用し、和の形で表すことができます。
ただし、斜辺は2重根号になっているので少々使いづらいです。
15°の三角比

こちらは30°の半角となっています。
こちらも22.5°と同じ手法で三角比を求めることができます。

今度は30°の三角形が見えてきました!
ということで、15°の三角比は、

こちらも斜辺が二重根号の形になっているので、斜辺は扱いづらいです。
まとめ
有名角やその半角の三角比についてよくわかったでしょうか。
高校以上であれば三角関数の加法定理や半角公式などを使って
求めているところを、
高校受験でいかにセンス良く求めていけるかがポイントでした!
今回は例題がありませんが、過去問などを活用して
三角比にチャレンジしてみてください!
前回の例題の答え
例題の答えをずっと公開していなかったのでここに書こうと思います。
2/26の例題
例題1
(1)
(2)
(3)
例題2
(1)
(2)
(3)
2/28の例題
【中学数学】ガウス記号ってなんだ?
好きな言葉は「被覆」。どうもこんにちは、ジャムです。
今回紹介するのは、
高校受験や大学受験で登場する摩訶不思議な記号、ガウス記号です。

"ガウス記号ってなに?"と思う方も少なくないと思います。
実際、ガウス記号は受験以外で見かけることはほとんどありません。
つまりガウス記号というのは、"受験数学の代名詞"、というわけです!
目次
そもそもガウス記号って?
この大括弧のような形をした記号は
受験数学では主にガウス記号なんて呼ばれますよね。
でも実はコレ、正式な名称ではありません。
でも存在しないわけでもないんですね。
実はガウス記号はもともと2つの関数だったんです。
・床関数(floor function)

床関数とは、ガウス記号と全く同じ意味を持ちますが、
記号は大括弧の上が欠けたような形をしています。
床関数ないしガウス記号の定義は、
実数
に対して
以下の最大の整数(wikiより)
と定義されています。
でも、この定義はすこ~し面倒くさいですよね。
ですから、
実数
の整数部分
と、覚えたほうが楽ですよ!(ただしが正の場合のみ)
また、この関数が整数部分を表しているということは、
は小数部分を表しているということになります!
ちなみに、この関数の整数部分という性質を利用して、
これを小数点以下切り捨てのプログラムとして
デジタル分野で使うことがあります。
・天井関数(ceiling function)

床に対して天井と、反対の名前を持つこの天井関数の定義は、
ガウス記号本来の定義と違っています。
大括弧の下が欠けたような形をしていますが、
ここも床関数と対象的な点です。
そんな天井関数の定義は、
実数
に対して
以上の最小の整数(wikiより)
となっています。
すでに勘のいい良い方は気づいているかもしれませんが、
床関数が"切り捨て"だったのに対し、天井関数は
"切り上げ"を意味しています。
ちなみに、ガウス記号はあくまで床関数と同義であり、
天井関数がガウス記号として出題されることはありません。
そのため、受験ではほとんど扱われません。
グラフ
・床関数(floor function)

ガウス記号ないし床関数のグラフは階段のような形をしています。
受験でこのグラフを描かせる問題はでませんが、
このグラフをイメージできていればガウス記号を押さえるのは
容易です!
・天井関数(floor function)

天井関数も床関数と同様、階段のような形をしています。
こちらも同様、受験で描かせるような問題は出ません。
・小数部分

個人的に、この関数に言及してみたかったので入れてみました。
この関数はが正の場合、その数の小数部分(
)を表しています。
この関数に特にこれと言った意味はないのですが、
実は、この関数はノコギリ波(sawtooth wave)の波形として
用いられることがあるんです。
(個人的にこのことが言いたかっただけ...)
例題
1つ例題を用意しましたので、良ければ解いてみてください!
追記:解答はこちらから jamjam1229.hatenablog.com
まとめ
今回は受験のみで登場するガウス記号を紹介しました!
今回始めてガウス記号を知った人も、過去に解いたことのある人も、
ガウス記号について深く知ることができたと思います!
例題の答えはいつか公開します!(前回の例題の答えもないような....?)
それでは!
【中学数学】受験で使える三角形の”心”
好きな言葉は「直交」。どうもこんにちは、ジャムです。
今回は、高校受験において頻出である三角形の"心”を
5つ紹介していきたいと思います!
三角形の”心”と書きましたが、これは三角形の五心のことです。
これらの避けては通れない五心を、利用した例を交えて
見ていきましょう!
目次
外心

外心とは三角形に外接する外接円の中心です。
この外接円の半径は三角形の相似を利用して算出できるので、
五心の中で最も重要な点とも言えます!
利用した例
外心を中心とする外接円の半径は、円周角の定理と、
三角形の相似を利用することで求められます。
(証明は長いので割愛します。)
内心

内心とは三角形に内接する内接円の中心です。
内接円の半径を利用することにより、三角形の面積を求めることが
でき、逆も可能です。
外心と並びよく出る点なので、性質を正しく理解しましょう!
利用した例
内接円の半径を利用して三角形の面積を求める際の公式があります。
垂心

垂心は各点の対辺へと垂直に下ろした直線の交点です。
五心の一つですが、中学数学ではこれと言った性質はありません。
そのため、五心の中での登場頻度は比較的少なめです。
利用した例
前述の通り、垂心には中学数学で説明できる段階で
特筆すべき性質はありません。
しかし、外心、内心と合わせてオイラー線という幾何的に
とても興味深い線を構成する点になります。
重心

重心とは、各点とその対辺の中点を結んだ直線(中線)の交点です。
数学の分野以外でも、
体の重心を....重心を前にして....など、日常でもよく耳にする単語です。 重心は他の4点と比べ少し複雑な点であるため、
入試問題でやや難関な問題として出題されることがあります。
また、いくつかの重要な性質があるので見ていきましょう。
利用した例
重心はそれぞれの中線を2:1に内分するという性質があります。

また、座標平面上の場合では、
重心の座標は、
という性質が成り立ちます。(すなわち、重心は三点の平均)
傍心

五心の中でも影の薄いこの傍心は、
厳密には三角形の心ではありませんが、
五心の中に入る重要な点です。
傍心は傍接円の中心の点のことで、傍接円とは、
三角形の外側にあり1辺と他の2辺の延長線に接する円のことです。
傍接円の半径を用いて三角形の面積を求めることもできるので、
傍心も忘れずに覚えておきましょう。
利用した例
傍接円の半径と面積に関する公式があります。
同様に、
まとめ
三角形の五心は垂心を除きすべて入試で役に立つものですので、
今回紹介した公式、性質は覚えておいて損はないと思います!
また、三角形の点は今回紹介した以外にも「フェルマー点」など、
まだたくさんのものがあります!
気になった方は調べてみてはいかがでしょうか?
それでは!
【中学数学】放物線と直線の組み合わせで使える裏ワザ
好きな言葉は「線形」。どうもこんにちは、ジャムです。
今回は中学数学のみで使える放物線のちょっとした裏ワザを
皆さんに紹介したいと思います。(厳密には、使えるけど限られる。)

放物線と直線の時短裏ワザ!
次のような直線と放物線があったとします。
(※図は超適当なのでちょっと変です。)

目的は直線の式を求めることです。
普通なら2つの座標を求めて、傾きを出して....
という流れのはずですよね。
さあ、少し考えてみてください。僕も考えます。
終わりましたか?前述の通りにやると恐らく30秒~1分程かかるはずです。
でもこれをたった3秒で求める方法があります。
しかもたった1つの式で表せます。知ってる人もいるかも。

ね?、簡単でしょ?
と、言ったもののこれだと形が複雑で覚えにくいですよね。
ということで、こう考えましょう。

僕はいつもこう考えています!(わかりにくくてすみません...)
ただ、この方法で覚えていると、たま~にaを忘れるので注意!
そして、上の計算式を使えば先程の問題はたった3秒で解けます
では、計算してみましょう!

・・・
はい、マジで3秒です。
こんな便利な公式が使えるなんて....数学に感謝しないと!
ということで感謝を表すため、証明します。
物線の式を、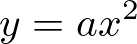 、直線の式を、
、直線の式を、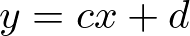 、直線との交点の
、直線との交点の![]() 座標を
座標を
値の小さい方から順に![]() とすると、
とすると、
直線の傾きは、
(q-p)%7D%7Bq-p%7D%3Da(p%2Bq)%0A%5Cend%7Balign*%7D&f=c&r=300&m=p&b=f&k=f)
切片は、
%20%5Ctimes%20p%20%2Bb%3Dap%5E2%5C%5C%0A%5CLeftrightarrow%20b%3Dap%5E2-ap%5E2-apq%5C%5C%0A%5CLeftrightarrow%20d%3D-apq%0A%5Cend%7Balign*%7D&f=c&r=300&m=p&b=f&k=f)
よって、この直線の式は
 ∎
∎
2つ例題をつくりましたので良ければ解いて見てください!
例題
例題1

上図のように、放物線 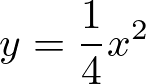 が、直線
が、直線 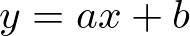 と、
と、%2CB(6%2C9)%0A%5Cend%7Balign*%7D&f=c&r=300&m=p&b=f&k=f) で
で
交わっているとき、次の問に答えよ。
(1)![]() の値を求めよ。
の値を求めよ。
(2)△![]() の面積を求めよ。
の面積を求めよ。
(3)点![]() よりも
よりも![]() 座標の小さい点
座標の小さい点![]() を放物線上にとり、
を放物線上にとり、
△![]() が△
が△![]() の面積と等しくなるとき、
の面積と等しくなるとき、
点![]() の
の![]() 座標を求めよ。
座標を求めよ。
例題2

上図のように、放物線 ![]() が、直線
が、直線 ![]() :
: 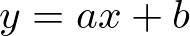 と、
と、%2CB(3%2C18)%0A%5Cend%7Balign*%7D&f=c&r=300&m=p&b=f&k=f) で,
で,
また、![]() に垂直な直線
に垂直な直線 ![]() :
: 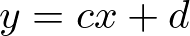 と
と![]() で交わっているとき、
で交わっているとき、
次の問に答えよ。
(1)![]() の値を求めよ。
の値を求めよ。
(2) ![]() の値を求めよ。
の値を求めよ。
(3)点![]() を新たにとり、四角形
を新たにとり、四角形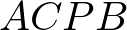 が平行四辺形となるとき、
が平行四辺形となるとき、
点![]() の座標を求めよ。
の座標を求めよ。
追記:例題の答えはこちらから
ちなみに
さて、実はこの公式、見方を変えれば
とても強力なもう一つの使い方ができるのです。
それは、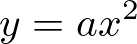 の形の二次関数に限り、微分ができます。
の形の二次関数に限り、微分ができます。
冗談じゃありません、微分です。
詳しい計算は省きますが、この公式が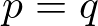 のとき直線は放物線と
のとき直線は放物線と
一点のみを接する線となります。そのとき、傾きは![]() という形になり、
という形になり、
これはまさしく元の関数を微分した形なのです!
中学数学恐ろしや(^^;
(※本来は傾きを出す過程で分母が0になるので解は存在しないはずなのだが、分母が約分によって消えてしまうので、うまい具合に微分ができてしまう。)