【中学数学】放物線と直線の組み合わせで使える裏ワザ
好きな言葉は「線形」。どうもこんにちは、ジャムです。
今回は中学数学のみで使える放物線のちょっとした裏ワザを
皆さんに紹介したいと思います。(厳密には、使えるけど限られる。)

放物線と直線の時短裏ワザ!
次のような直線と放物線があったとします。
(※図は超適当なのでちょっと変です。)

目的は直線の式を求めることです。
普通なら2つの座標を求めて、傾きを出して....
という流れのはずですよね。
さあ、少し考えてみてください。僕も考えます。
終わりましたか?前述の通りにやると恐らく30秒~1分程かかるはずです。
でもこれをたった3秒で求める方法があります。
しかもたった1つの式で表せます。知ってる人もいるかも。

ね?、簡単でしょ?
と、言ったもののこれだと形が複雑で覚えにくいですよね。
ということで、こう考えましょう。

僕はいつもこう考えています!(わかりにくくてすみません...)
ただ、この方法で覚えていると、たま~にaを忘れるので注意!
そして、上の計算式を使えば先程の問題はたった3秒で解けます
では、計算してみましょう!

・・・
はい、マジで3秒です。
こんな便利な公式が使えるなんて....数学に感謝しないと!
ということで感謝を表すため、証明します。
物線の式を、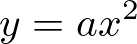 、直線の式を、
、直線の式を、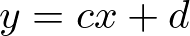 、直線との交点の
、直線との交点の![]() 座標を
座標を
値の小さい方から順に![]() とすると、
とすると、
直線の傾きは、
(q-p)%7D%7Bq-p%7D%3Da(p%2Bq)%0A%5Cend%7Balign*%7D&f=c&r=300&m=p&b=f&k=f)
切片は、
%20%5Ctimes%20p%20%2Bb%3Dap%5E2%5C%5C%0A%5CLeftrightarrow%20b%3Dap%5E2-ap%5E2-apq%5C%5C%0A%5CLeftrightarrow%20d%3D-apq%0A%5Cend%7Balign*%7D&f=c&r=300&m=p&b=f&k=f)
よって、この直線の式は
 ∎
∎
2つ例題をつくりましたので良ければ解いて見てください!
例題
例題1

上図のように、放物線 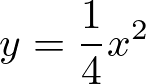 が、直線
が、直線 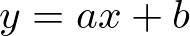 と、
と、%2CB(6%2C9)%0A%5Cend%7Balign*%7D&f=c&r=300&m=p&b=f&k=f) で
で
交わっているとき、次の問に答えよ。
(1)![]() の値を求めよ。
の値を求めよ。
(2)△![]() の面積を求めよ。
の面積を求めよ。
(3)点![]() よりも
よりも![]() 座標の小さい点
座標の小さい点![]() を放物線上にとり、
を放物線上にとり、
△![]() が△
が△![]() の面積と等しくなるとき、
の面積と等しくなるとき、
点![]() の
の![]() 座標を求めよ。
座標を求めよ。
例題2

上図のように、放物線 ![]() が、直線
が、直線 ![]() :
: 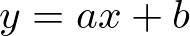 と、
と、%2CB(3%2C18)%0A%5Cend%7Balign*%7D&f=c&r=300&m=p&b=f&k=f) で,
で,
また、![]() に垂直な直線
に垂直な直線 ![]() :
: 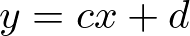 と
と![]() で交わっているとき、
で交わっているとき、
次の問に答えよ。
(1)![]() の値を求めよ。
の値を求めよ。
(2) ![]() の値を求めよ。
の値を求めよ。
(3)点![]() を新たにとり、四角形
を新たにとり、四角形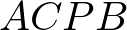 が平行四辺形となるとき、
が平行四辺形となるとき、
点![]() の座標を求めよ。
の座標を求めよ。
追記:例題の答えはこちらから
ちなみに
さて、実はこの公式、見方を変えれば
とても強力なもう一つの使い方ができるのです。
それは、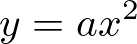 の形の二次関数に限り、微分ができます。
の形の二次関数に限り、微分ができます。
冗談じゃありません、微分です。
詳しい計算は省きますが、この公式が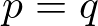 のとき直線は放物線と
のとき直線は放物線と
一点のみを接する線となります。そのとき、傾きは![]() という形になり、
という形になり、
これはまさしく元の関数を微分した形なのです!
中学数学恐ろしや(^^;
(※本来は傾きを出す過程で分母が0になるので解は存在しないはずなのだが、分母が約分によって消えてしまうので、うまい具合に微分ができてしまう。)